One of the purest and most fascinating examples of the “wisdom of crowds” in action comes courtesy of a unique online contest called ProbabilitySports run by mathematician Brian Galebach.
In the contest, each participant states how likely she thinks it is that a team will win a particular sporting event. For example, one contestant may give the Steelers a 62% chance of defeating the Seahawks on a given day; another may say that the Steelers have only a 44% chance of winning. Thousands of contestants give probability judgments for hundreds of events: for example, in 2004, 2,231 ProbabilityFootball participants each recorded probabilities for 267 US NFL Football games (15-16 games a week for 17 weeks).
An important aspect of the contest is that participants earn points according to the quadratic scoring rule, a scoring method designed to reward accurate probability judgments (participants maximize their expected score by reporting their best probability judgments). This makes ProbabilitySports one of the largest collections of incentivized1 probability judgments, an extremely interesting and valuable dataset from a research perspective.
The first striking aspect of this dataset is that most individual participants are very poor predictors. In 2004, the best score was 3747. Yet the average score was an abysmal -944 points, and the median score was -275. In fact, 1,298 out of 2,231 participants scored below zero. To put this in perspective, a hypothetical participant who does no work and always records the default prediction of “50% chance” for every team receives a score of 0. Almost 60% of the participants actually did worse than this by trying to be clever.
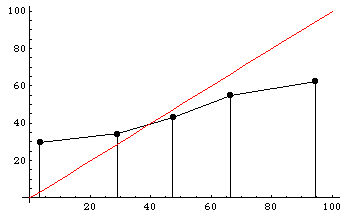Participants are also poorly calibrated. To the right is a histogram dividing participants’ predictions into five regions: 0-20%, 20-40%, 40-60%, 60-80%, and 80-100%. The y-axis shows the actual winning percentages of NFL teams within each region. Calibrated predictions would fall roughly along the x=y diagonal line, shown in red. As you can see, participants tended to voice much more extreme predictions than they should have: teams that they said had a less than 20% chance of winning actually won almost 30% of the time, and teams that they said had a greater than 80% chance of winning actually won only about 60% of the time.
Yet something astonishing happens when we average together all of these participants’ poor and miscalibrated predictions. The “average predictor”, who simply reports the average of everyone else’s predictions as its own prediction, scores 3371 points, good enough to finish in 7th place out of 2,231 participants! (A similar effect can be seen in the 2003 ProbabilityFootball dataset as reported by Chen et al. and Servan-Schreiber et al.)
Even when we average together the very worst participants — those participants who actually scored below zero in the contest — the resulting predictions are amazingly good. This “average of bad predictors” scores an incredible 2717 points (ranking in 62nd place overall), far outstripping any of the individuals contributing to the average (the best of whom finished in 934th place), prompting someone in this audience to call the effect the “wisdom of fools”. The only explanation is that, although all these individuals are clearly prone to error, somehow their errors are roughly independent and so cancel each other out when averaged together.
Daniel Reeves and I follow up with a companion post on Robin Hanson’s OvercomingBias forum with some advice on how predictors can improve their probability judgments by averaging their own estimates with one or more others’ estimates.
In a related paper, Dani et al. search for an aggregation algorithm that reliably outperforms the simple average, with modest success.
| Â Â Â Â | 1Actually the incentives aren’t quite ideal even in the ProbabilitySports contest, because only the top few competitors at the end of each week and each season win prizes. Participants’ optimal strategy in this all-or-nothing type of contest is not to maximize their expected score, but rather to maximize their expected prize money, a subtle but real difference that tends to induce greater risk taking, as Steven Levitt describes well. (It doesn’t matter whether participants finish in last place or just behind the winners, so anyone within striking distance might as well risk a huge drop in score for a small chance of vaulting into one of the winning positions.) Nonetheless, Wolfers and Zitzewitz show that, given the ProbabilitySports contest setup, maximizing expected prize money instead of expected score leads to only about a 1% difference in participants’ optimal probability reports. |
It would be interesting to see if the public is able to make good collective judgments on other things besides sports. The last presidential election makes me skeptical of that, but perhaps the electoral college distorts the results.
Somone asked me over email to include the results for the “average of good experts” (AOG), meaning the average of experts who scored above zero. In 2004 AOG scores 3829 points: better than the best individual expert. However this is NOT an actionable strategy: we could not have entered AOG in the contest. AOG identifies the good experts after the fact, after the end of the contest. An actionable strategy that tries to identify the good experts “along the way”, according to past predictions, doesn’t seem to do nearly as well, at least not consistently, and at least not for the many methods we’ve tried.
This is very interesting. In a true prediction market, as i understand it, you must have a buyer and a seller. So, for every 80% there must be a 20% willing to make a deal. So, it seems, that would limit the ability of experts to participate in the ‘market’. If the market price is 80% for the chargers to win, I cannot but a 70% very easily.
Of course, I may be missing something.
That’s correct. Though note that ProbabilitySports is not a prediction market, but rather a contest based on socring rules, so anyone can submit any probability that they want — there is no matching required.
Of course, the mentioned expert would participate in the 80/20 contract because he thinks the 20 is a bargain! So, what i really meant to point out was that the prediction-market (TradeSports for example) does not capture the same data about what experts really think about the probabilities.
Dave indirectly pointed me to a new paper by Lichtendahl and Winkler at Duke (“Probability Elicitation, Scoring Rules, and Competition among Forecasters”) that gives a model in which participants care about their rank order in the contest as well as the raw payment from the scoring rule. In that model the miscalibration may in fact be rational, rather than overconfidence bias.
I think this points to the need for meaningful payment in prediction markets!
So I guess my question is, is there any way to take that information you laid out and use it to one’s advantage? I have always been interested in mathematical formulas, so I was just curious about your perspective.
BeatVegasLine.com ask users to pick the winning team versus the vegas line and presents the picks as pie charts. Does this meet the requirements for a valid “Wisdom Of The Crowd” experiment?
This is very interesting. In a true prediction market, as i understand it, you must have a buyer and a seller. So, for every 80% there must be a 20% willing to make a deal. So, it seems, that would limit the ability of experts to participate in the ‘market’. If the market price is 80% for the chargers to win, I cannot but a 70% very easily.
Of course, I may be missing something.