What exactly is a combinatorial prediction market?

2010 Update: Several of us at Yahoo! Labs, along with academic researchers, have theorized and written about combinatorial prediction markets for several years, as you’ll see below. But now we’ve gone beyond talking about them and actually built one. So the best way to answer the question is to see the market we built and play with it. It’s called Predictalot. The first version was based on the NCAA Men’s College Basketball tournament known as March Madness.

Combinatorial Madness

March Madness is the anything-can-happen-and-often-does tournament among the top 64 NCAA Men’s College Basketball teams. The “madness” of the games is rivaled only by the madness of fans competing to pick the winners. In Las Vegas, you can bet on many things, from individual games to the overall champion to more exotic “propositions” like which conference of teams will do best. Still, each gambling venue defines in advance exactly what you are allowed to bet on, offering an explicit list of usually no more than a few thousand choices.

So here is my informal definition: a combinatorial market is one where users can construct their own bets by mixing and matching options in myriad ways, sort of like ordering a Wendy’s hamburger. (Or highly customized insurance.)

The Details

Now I’ll try for a more precise definition.

Just to set the vocabulary straight, outcomes are all possible things that might happen: for example all five candidates in an election, all 30 teams in an NBA Championship market, all 3,628,800 (or 10!) finish orderings in a ten-horse race, or all 9.2 quintillion March Madness tournament results. Among the outcomes, in the end one and only one of them will actually occur; traders try to predict which.

Bids express what outcome(s) traders think will happen. Bids also contain the risk-reward ratio the trader is willing to accept: the amount she wins if correct and the amount she is willing to lose if incorrect.

There are two reasons why we might call a market “combinatorial”: either the bids are combinatorial or the outcomes are combinatorial. The latter poses a much harder computational problem. I’ll start with the former.

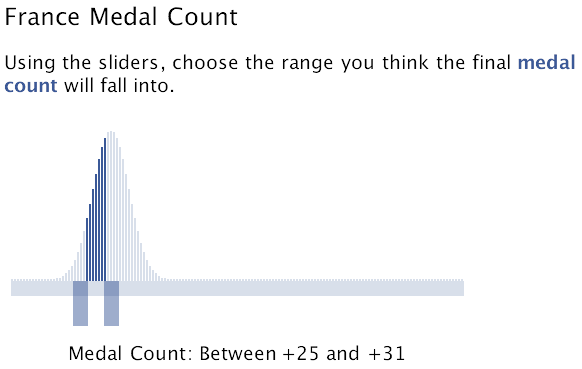
1. Combinatorial bids. A combinatorial bid or bundle bid is a concise expression representing a collection or set of outcomes, for example “a Western Conference team will win the NBA Championship”, encompassing 15 possible outcomes, or “horse A will finish ahead of horse B” in a ten-horse race, encoding 1,814,400, or half, of the possible outcomes. Yoopick, our experimental sports prediction market on Facebook, features a type of combinatorial bidding called interval bidding. Traders select the range they think the final score difference will fall into, for example “Pittsburgh will win by between 2 and 11 points”. An interval bet is actually a collection of bets on every outcome between the left and right endpoints of the range.

   For comparison, a non-combinatorial bid is a bet on a single outcome, for example “candidate O will win the election”. The vast majority of fielded prediction markets handle only non-combinatorial bids.

   What are examples of combinatorial bids besides Yoopick? Abe Othman built an interval betting interface similar to Yoopick (he came up with it on his own, proving that great minds think alike) to predict when the new CMU computer science building will finish construction. Additional examples include Bossaerts et al.’s concept of combined value trading and the parimutuel call market mechanism [Baron & Lange, Lange & Economides, Peters et al.]. 2010 Update: Predictalot is our latest example of a market featuring both combinatorial bids and outcomes.

2. Combinatorial outcomes. The March Madness scenario is an example of combinatorial outcomes. The number of outcomes (e.g., 9.2 quintillion) may be so huge that we could never hope to track every outcome explicitly inside a computer. Instead, outcomes themselves are defined implicitly according to some counting process that involves enumerating every possible combination of base objects. For example, the outcome space could be all n! possible finish orderings of an n-horse race. Or all 2ⁿ combinations of n binary events. In both cases, the number of outcomes grows exponentially in the number of base objects n, quickly becoming unimaginably large as n grows.

   A market with combinatorial outcomes is almost nonsensical without allowing combinatorial bids as well, since individual outcomes are like microbes on a needle on a cruise ship of hay in a universe-sized sea. No one wants to bet on these minuscule possibilities one at a time. Instead, traders bet on high-level properties of outcomes, like “Duke will advance further than UNC”, that encode sets of outcomes. Here are some example forms of combinatorics and corresponding bidding languages that seem natural:

   • Boolean betting. Outcomes are combinations of binary events. Bids are phrased in Boolean logic. So if base objects are “Democrat will win in Alabama”, “Democrat will win in Alaska”, etc. for all fifty US states, and outcomes are all 2⁵⁰ possible ways the election might swing across all 50 states, then bids may be of the form “Democrat will win in Ohio and Florida, but not Virginia”, or “Democrat will win Nevada if they win California”, etc. For further reading, see Hanson’s paper on combinatorial market makers and our papers on the computational complexity of Boolean betting auctioneers and market makers.
   • Tournament betting. This is the March Madness example and a special case of Boolean betting. See our paper on tournament betting market makers.
   • Permutation betting. Outcomes are possible finish orderings in a horse race. Bids are properties of orderings, for example “Horse B will finish ahead of horse D”, or “Horse B will finish between 3rd and 7th place”. See our papers on permutation betting auctioneers and market makers.
   • Taxonomy betting. Base objects are (discretized) numbers arranged in a taxonomy, for example web site page views organized by topic, subtopic, etc. Outcomes are all possible combinations of the numbers. Bets can be placed on the range of any number in the taxonomy, for example page views of a sports web site, page views of the NBA subsection of the web site, etc. Coming soon: a paper on taxonomy betting led by Mingyu Guo at Duke. [Update: here is the paper.]

   We summarize some of these in a short article on Combinatorial betting and a more detailed book chapter on Computational aspects of prediction markets.

   2009 Update: Gregory Goth writes an excellent and accessible summary in the March 2009 Communcations of the ACM, p.13.

Auctioneer versus market maker

So far, I’ve only talked about the form of bids from traders. Next I’ll discuss the actual mechanics of the marketplace, or how bids are processed. How does the market operator decide which bids to accept or reject? At what prices?

I’ll focus on two major possibilities: either the market operator acts as an auctioneer or he acts as an automated market maker.

An auctioneer only matches up willing traders with each other — the auctioneer never takes on any risk of his own. This is how most financial exchanges like the stock market operate, and how intrade and betfair operate. (A call market is a special case where the auctioneer collects many bids over a period of time, then processes them all together in a single batch.)

An automated market maker will quote a price for any bet whatsoever. Even lone traders can place their bet with the market maker as long as they accept the price, greatly enhancing liquidity. The liquidity comes at a cost though: an automated market maker can and often does lose money, though clever pricing algorithms can guarantee that losses won’t mount beyond a fixed amount set in advance. Hanson’s logarithmic market scoring rule market maker is far and away the most popular for prediction markets, and for good reason: it’s simple, has nice modularity properties, and behaves well in practice. We catalog a number of bounded-loss market makers in this paper. The dynamic parimutuel market used in the (now closed) Yahoo! Tech Buzz Game can be thought of as another type of automated market maker.

A market with combinatorial outcomes almost requires a market maker to function smoothly. When traders have such a mind-boggling array of choices, the chances that two or more of their bets will exactly counter each other seems remote. If trades are rarely filled, then traders won’t bother bidding at all, causing a no-chicken-no-egg spiral into failure.

One the other hand, a market maker allows anyone to get a price quote at any time on any bet, no matter how convoluted or specific, even if no other traders had thought about that particular possibility. Thus interacting with a combinatorial market maker can be highly satisfying: propose any obscure proposition, click “accept price”, and your bet is placed: no doubt and no waiting.

I’ll discuss one more technicality. An auctioneer must decide whether bids can be partially filled, giving traders both less risk and less reward than they requested, in the same ratio. This makes sense. If I’m willing to risk $100 to win $200, I’d almost surely risk $50 to win $100 instead. Allowing partial fills greatly simplifies life for the auctioneer too. If bids are divisible, or can be filled in part, the auctioneer can use efficient linear programming algorithms; if bids are indivisible, the auctioneer must use integer programming algorithms that may be intractable. For more on the divisible/indivisible distinction, see Bossaerts et al. and Fortnow et al. Allowing divisible bids seems the logical choice in most scenarios, since the market functions better and most traders won’t mind.

The benefits of combinatorial markets

Why do we need or want combinatorial markets? Simply put, they allow for the collection of more information, the life-blood of every prediction market. Combinatorial outcomes allow traders to assess the correlations among base objects, not just their independent likelihoods, for example the correlation between Democrats winning in Ohio and Pennsylvania. Understanding correlations is key in many applications, including risk assessment: one might argue that the recent financial meltdown is partly attributable to an underestimation of correlation among firms and securities and the chances of cascading failures.

Although financial and betting exchanges, bookmakers, and racetracks are modernizing, turning their operations over to computers and moving online, their core logic for processing bids hasn’t changed much since auctioneers were people. For simplicity, they treat all bets like apples and oranges, processing them independently, even when they are more like hamburgers and cheeseburgers. For example, bets on a horse “to win” and “to finish in the top two” are managed separately at the racetrack, as are options to buy a stock at “strike price 30” and “strike price 20” on the CBOE. In both cases it’s a logical truism that the first is worth less than the second, yet the market pleads ignorance, leaving it to traders to enforce consistent pricing.

In a combinatorial market, a bet on “Duke will win the tournament” automatically increases the odds on “Duke will win in the first round”, as it logically should. Mindless mechanical tasks like this are handled automatically, by algorithms that are far better at it anyway, freeing up traders for the primary task a prediction market asks them to do: provide information. Traders are free to express their information in whatever form they find most natural, and it all flows into the same pool of liquidity.

I discuss the benefits of combinatorial bids further in this post, including one benefit I don’t mention here: smarter accounting, or making sure no more is reserved from a trader’s balance than necessary to cover their worst-case loss.

The disadvantages of combinatorial markets

I would argue that there is virtually no disadvantage to allowing combinatorial bids. They are more flexible and natural for traders, and they eliminate redundancy and thus concentrate liquidity (again I refer the reader to this previous post). Allowing indivisible combinatorial bids can cause computational problems, but as I argue above, divisible bids make more sense anyway.

On the other hand, there can be disadvantages to markets with combinatorial outcomes. First, trader attention and liquidity may be severely fractured, since there are nearly limitless things to bet on.

Second, and perhaps more troublesome, running an auctioneer with combinatorial outcomes is computationally intractable (specifically, NP-hard, or as hard as solving SAT) and running a market maker is even harder (specifically, #P-hard, as hard as counting SAT), meaning that the amount of time needed to run is proportional to the number of outcomes, exponential in the number of objects.

It gets worse. Even if we place strict limits on what types of bets traders can make, the market may still be infeasible to run. For example, even if all bets are pairwise, like “Horse B will finish ahead of horse D”, the auctioneer and market maker problems for permutation betting remain NP-hard and #P-hard, respectively. Likewise, Boolean betting remains hard even if the most complicated bet allowed is joining two events, like “E will happen and F will not” [see Chen et al. and Fortnow et al.].

How to build one

Now for some good news: in some cases, fast algorithms are possible. If all bets are subset bets of the form “Horse A will finish in position 1,2, or 10” or “Horse B,C, or E will finish in position 3”, then permutation betting with an auctioneer is feasible (using a combination of linear programming and maximum matching), even though the corresponding market maker problem is #P-hard. If all bets are of the form “Team B will advance to round k”, tournament betting with a market maker is feasible (using Bayesian network inference). Taxonomy betting with a market maker is feasible (using dynamic programming).

Finally, even better news: fast market maker approximation algorithms are not only possible and practical, they work without limiting what people can bet on, fulfilling the almost magical promise I made at the outset of constructing any bet you can imagine on the fly. Approximation works because people like to bet on things that have a decent chance of happening, say between a 1% and 99% chance. Standard sampling algorithms, including importance sampling and MCMC, are good at approximating prices for such reasonable events. For the extreme (e.g., 1-in-a-billion) events, sampling may fail, so the market maker will have to round off in its own favor to be safe.

Wrapping up, in my mind, the best way to implement a combinatorial-outcome prediction market is as follows:

• Use a market maker. Without one, traders are unlikely to find each other in the sea of choices. Specifically, use Hanson’s LMSR market maker.
• Use an approximation algorithm for pricing. Importance sampling seems to work well. MCMC is another possibility. See Appendix A of this paper.
• The interface is absolutely key, and the aspect I’m least qualified to opine on. I think Predictalot, WeatherBill, Yoopick, and WhenWillWeMove point in the right direction.

2010 Update: Predictalot is our first pass at carrying through on this vision of how to build a combinatorial prediction market. In building it, we learned a great deal already, for example that sampling is much much trickier than I had initially imagined, and that it’s easy to accidentally create arbitrage loopholes if you’re not extremely careful with the math.

I glossed over a number of details. For example, care must be taken for the market maker to always round approximations in its own favor to avoid opening itself up to arbitrage attacks. Another difficulty is how to implement smart accounting to allow traders maximum leverage when they place many interrelated bets. The assumption that traders could lose all their bets is far too conservative — they might have bets that provably cannot simultaneously lose — but may serve as a reasonable starting point in practice.