This is the first of a series of challenge posts. I’ll pose a problem in the hopes of convincing the wise Internauts to come forth with solutions. I intend the problems to be do-able rather than mind boggling: simply intriguing problems that I’d love to know the answer to but haven’t found the time yet to work through. Think of it as Web 2.0 enlightenment mixed with good old fashioned laziness. Or think of it as Yahoo! Answers, blog edition.
Don’t expect to go unrewarded for your efforts! I’ll pay ten yootles, plus an optional and unspecified tip, to the respondent with the best solution. What can you do with these yootles? Well, to make a long story short, you can spend them with me, people who trust me, people who trust people who trust me, etc. (In lieu of a formal microformat specification for yootles offers, for now I’ll simply use the keyword/tag “yootleoffer” to identify opportunities to earn yootles, in the spirit of “freedbacking”.)
 So, on with the challenge! I just returned from a pit stop in Las Vegas, so this one is weighing on my mind. I’d like to see an analysis of strategies for playing craps that take into account the variance of the bettor’s wealth, not just the expectation.
So, on with the challenge! I just returned from a pit stop in Las Vegas, so this one is weighing on my mind. I’d like to see an analysis of strategies for playing craps that take into account the variance of the bettor’s wealth, not just the expectation.
Every idiot knows the best strategy to minimize the casino’s edge in craps: bet the pass line and load up on the maximum odds possible. The odds bet in craps is one of the only fair bets in the casino, so the more you load up on odds, the closer the casino’s edge is to zero. But despite the fact that craps is one of the fairest games on the casino floor, it’s also one of the highest variance games, meaning that your money can easily swing wildly up or down in a manner of minutes. So on a fixed budget, craps can be exceedingly dangerous. What I’m looking for is one or more strategies that have lower variance, and are thus less risky.
So that this challenge is not vague and open ended, let me boil this overall goal down into something fairly specific:
The Challenge: Suppose that I walk into a casino with $200. I arrive at a craps table that has a $5 minimum bet and allows 2X odds. I’m looking for a strategy that:
|
I prefer if you ignore the center bets in your analysis. Bonus points if you examine what happens with different budgets, table limits, and/or allowed odds. Another way to motivate this is as follows: I have a small fixed budget but want to hang around a high-limit table for as long as possible, because I get a better atmosphere, more drinks, and a glimpse of life as a high roller.
As an example, here is a strategy that appears to have very low variance: On the come out roll, bet on both the pass line and the don’t pass line. If the shooter rolls 2, 3, 7, or 11 you break even. If the shooter rolls 4, 5, 6, 8, 9, or 10, you’re also guaranteed to eventually break even. The only time you lose money is when the shooter rolls a 12 on a come out roll, in which case you lose your pass line bet and keep your don’t pass bet (i.e., you lose half your total stake). There’s only one problem with this strategy: it’s moronic. You have absolutely no possibility of winning: you can only either break even or lose. One thing you might add to this strategy to satisfy condition (1) is to take or give odds whenever the shooter establishes a point. Will this strategy make my $200 last longer on average than playing the pass line only?
For bonus points, I’d love to see a graph plotting a number of different strategies along the efficient frontier, trading off casino edge and variance. Another bonus point question: In terms of variance, is it better to place a single pass line bet with large odds, or is it better to place a number of come bets all with smaller odds?
To submit your answer to this challenge, post a comment with a link to your solution. If you can dig up the answer somewhere on the web, more power to you. If you can prove something analytically, I bow to you. Otherwise, I expect this to require some simple Monte Carlo simulation. Followed of course by some Monte Carlo verification. 🙂 Have fun!
Addendum: The winner is … Fools Gold!
 If a
If a  I finally read Time Magazine’s 2006 Person of the Year issue (as usual, I’m a month behind
I finally read Time Magazine’s 2006 Person of the Year issue (as usual, I’m a month behind 
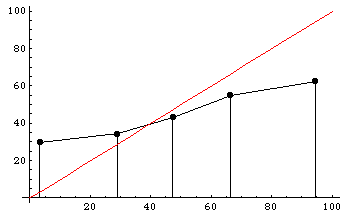 Participants are also poorly calibrated. To the right is a histogram dividing participants’ predictions into five regions: 0-20%, 20-40%, 40-60%, 60-80%, and 80-100%. The y-axis shows the actual winning percentages of NFL teams within each region. Calibrated predictions would fall roughly along the x=y diagonal line, shown in red. As you can see, participants tended to voice much more extreme predictions than they should have: teams that they said had a less than 20% chance of winning actually won almost 30% of the time, and teams that they said had a greater than 80% chance of winning actually won only about 60% of the time.
Participants are also poorly calibrated. To the right is a histogram dividing participants’ predictions into five regions: 0-20%, 20-40%, 40-60%, 60-80%, and 80-100%. The y-axis shows the actual winning percentages of NFL teams within each region. Calibrated predictions would fall roughly along the x=y diagonal line, shown in red. As you can see, participants tended to voice much more extreme predictions than they should have: teams that they said had a less than 20% chance of winning actually won almost 30% of the time, and teams that they said had a greater than 80% chance of winning actually won only about 60% of the time.